中考数学之规律与探索专题

工作比较忙，已经有一段时间没有发文了，今天给大家来讲讲如何复习规律与探索相关专题。

什么是规律与探索相关专题？

规律与探索问题一般指的是给出一定条件(可以是有规律的算式、图形或图表)，通过认真分析，仔细观察，综合归纳，大胆猜想，进而得出结论，并加以验证的数学探索题。

直白的讲，规律与探索问题就是指给出一定条件(可以是有规律的算式、图形或图表)，让学生认真分析，仔细观察，综合归纳，大胆猜想，得出结论，进而加以验证的数学探究题。

中考数学规律与探索专题，典型例题分析1：

在直角坐标系中，正方形A₁B₁C₁O₁、A₂B₂C₂C₁、…、A_nB_nC_nC_n-1按如图所示的方式放置，其中点A₁、A₂、A₃、…、A_n均在一次函数y=kx+b的图象上，点C₁、C₂、C₃、…、C_n均在x轴上．若点B₁的坐标为（1，1），点B₂的坐标为（3，2），则点A_n的坐标为 .

考点分析：

一次函数综合题；相似三角形的判定与性质；规律型。

题干分析：

首先求得直线的解析式，分别求得A₁，A₂，A₃…的坐标，可以得到一定的规律，据此即可求解。

解题反思：

本题主要考查了待定系数法求函数解析式，正确得到点的坐标的规律是解题的关键。

规律与探索问题几乎是全国很多地方中考数学的必考题型之一，一般会以选择题或填空题的形式出现，某些地方甚至会以解答题形式考查考生，所占的分值较高，大家应多加关注。

规律与探索问题一般有三大类题型，分别是数字类型、列代数式类型、图形规律变化类型。

要想准确解决此类问题，就要抓住其解题思路，如它的解题思维过程一般是从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论。

中考数学规律与探索专题，典型例题分析2：

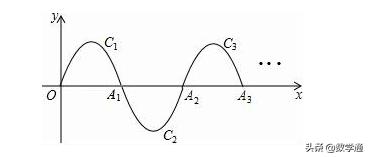
如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C₁，它与x轴交于两点O，A₁；将C₁绕A₁旋转180°得到C₂，交x轴于A₂；将C₂绕A₂旋转180°得到C₃，交x轴于A₃；…如此进行下去，直至得到C₆，若点P（11，m）在第6段抛物线C₆上，则m= ．

解：∵y=﹣x（x﹣2）（0≤x≤2），

∴配方可得y=﹣（x﹣1）²+1（0≤x≤2），

∴顶点坐标为（1，1），

∴A₁坐标为（2，0）

∵C₂由C₁旋转得到，

∴OA₁=A₁A₂，即C₂顶点坐标为（3，﹣1），A₂（4，0）；

照此类推可得，C₃顶点坐标为（5，1），A₃（6，0）；

C₄顶点坐标为（7，﹣1），A₄（8，0）；

C₅顶点坐标为（9，1），A₅（10，0）；

C₆顶点坐标为（11，﹣1），A₆（12，0）；

∴m=﹣1．

故答案为：﹣1．

考点分析：

二次函数图象与几何变换；抛物线与x轴的交点；规律型。

题干分析：

将这段抛物线C₁通过配方法求出顶点坐标及抛物线与x轴的交点，由旋转的性质可以知道C₁与C₂的顶点到x轴的距离相等，且OA₁=A₁A₂，照此类推可以推导知道点P（11，m）为抛物线C₆的顶点，从而得到结果。

解题反思：

本题考查了二次函数的性质及旋转的性质，解题的关键是求出抛物线的顶点坐标。

结合相关题型和解题思路，我们发现规律与探索问题对学生的思维能力又一定要求，同时学生通过此类题型的训练，能提高自身思维方式、能力等各方面的深刻性和创造性。

解决规律与探索问题难度相对较小，要善于从所提供的数字或图形信息中，寻找其共同之处，这个存在于个例中的共性，就是规律。这体现化归转化思想，既“特殊——一般——特殊”的常用模式，这也正是人类认识探索未知领域的一般过程。

中考数学规律与探索专题，典型例题分析3：

已知世运会．亚运会．奥运会分别于公元2009年．2010年．2012年举办．若这三项运动会均每四年举办一次，则这三项运动会均不在下列哪一年举办？（ ）

A．公元2070年 B．公元2071年 C．公元2072年 D．公元2073年

解：A．2070－2009＝61，

2070－2010＝60，

2070－2012＝58，其中60是4的倍数，所以亚运会能在2070年举办，则世运会在2069年．奥运会在2072年举办．

B．2071－2009＝62，

2071－2010＝61，

2071－2012＝59，均不是4的倍数，所以，这三项运动会均不在2071年举办．

C．2072－2009＝63，

2072－2010＝62，

2072－2012＝60，60是4的倍数，所以奥运会能在2072年举办，则世运会在2069年．亚运会在2070年举办．

D．2073－2009＝64，

2073－2010＝63，

2073－2012＝61，64是4的倍数，所以世运会能在2073年举办，则亚运会在2074年．奥运会在2076年举办．

故选：B．

考点分析：

规律型；数字的变化类。

题干分析：

由已知，我们可总结出每4年举办一次，只要每个选项与2009，2010，2012的差有一个是4的倍数，则能在这一年此项运动会，否则这三项运动会均不在这一年举办。

解题反思：

此题考查的知识点是数字变化类问题，解题的关键是要通过每4年举办一次，求出每个选项与2009，2010，2012的差，看是否有4的倍数确定答案。

解决规律与探索类问题，要学会把直观猜想与科学论证、具体应用相结合，掌握一些常规的解题方法，如计算、验证、类比、比较、测量、绘图、移动等等。

中考数学规律与探索专题，典型例题分析4：

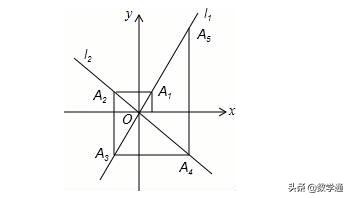
如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l₁，l₂，过点（1，0）作x轴的垂线交l₂于点A₁，过点A₁作y轴的垂线交l₂于点A₂，过点A₂作x轴的垂线交l₂于点A₃，过点A₃作y轴的垂线交l₂于点A₄，…依次进行下去，则点A₂₀₁₇的坐标为　 　

解：观察，发现规律：A₁（1，2），A₂（﹣2，2），A₃（﹣2，﹣4），A₄（4，﹣4），A₅（4，8），…，

∴A_2n+1（（﹣2）ⁿ，2（﹣2）ⁿ）（n为自然数）．

∵2017=1008×2+1，

∴A₂₀₁₇的坐标为（（﹣2）¹⁰⁰⁸，2（﹣2）¹⁰⁰⁸）=（2¹⁰⁰⁸，2¹⁰⁰⁹）．

故答案为：（2¹⁰⁰⁸，2¹⁰⁰⁹）．

考点分析：

一次函数图象上点的坐标特征；规律型；一次函数及其应用．

题干分析：

写出部分A_n点的坐标，根据坐标的变化找出变化规律“A_2n+1（（﹣2）ⁿ，2（﹣2）ⁿ）（n为自然数）”，依此规律即可得出结论。

解题反思：

本题考查了一次函数图象上点的坐标特征以及规律型中坐标的变化，解题的关键是找出变化规律“A_2n+1（（﹣2）ⁿ，2（﹣2）ⁿ）（n为自然数）”。本题属于基础题，难度不大，解决该题型题目时，写出部分A_n点的坐标，根据坐标的变化找出变化规律是关键。

解决规律与探索类问题，要学会能从题目中的图形或者数字直观地发现共同特征，或者发展变化的趋势，通过观察、归纳，探索发现这些图形或数字所蕴藏的数学本质，必要时可以进行验证或者证明。

大家一定要清醒认识到猜想和探索不仅仅是一种重要数学研究方法，更是人类探索未知领域的重要手段，因此，与规律与探索类相关问题一直是中考数学的热点。