巧用辅助圆 妙解几何题（中考辅导）

辅助线的添加是几何解题的关键和难点，是学生学习数学常用的手段，进行几何解题时，准确的添加辅助线可以使问题迎刃而解，初中几何在添加辅助线时普遍存在重“直”轻“曲”的现象，尤其是辅助圆的添加，学生更是难以接受，圆的定义虽貌似平平，但表达形式多样，我们结合圆的定义和判定特征，巧妙地引入辅助线，转化为利用圆的几何性质来解决，往往全使问题思路豁然开朗，运算简单便捷。

模型1 共端点，等线段模型

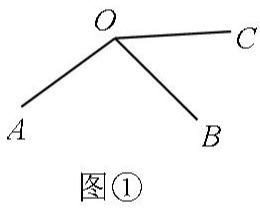
如图①，出现“共端点，等线段”时，可利用圆定义构造辅助圆．

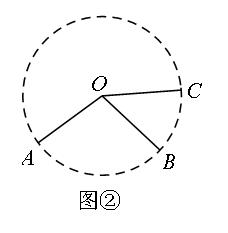
如图②，若OA＝OB＝OC，则A、B、C三点在以O为圆心，OA为半径的圆上．

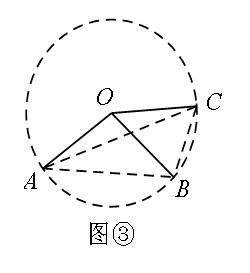
如图③常见结论有∠AOB＝2∠ACB，∠BOC＝2∠BAC.

例1 如图，△ABC,△ACD都是等腰三角形，AB=AC=AD,连接BD,求证：∠1+∠2=90°

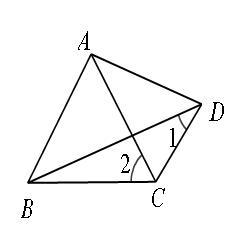
证明：∵AB＝AC＝AD．∴B、C、D在以A为圆心，AB为半径的⊙A上．∴∠ABC＝∠2.

在△BAC中，∵∠BAC＋∠ABC＋∠2＝180°,∴2∠1＋2∠2＝180°.

∴∠1＋∠2＝90°.

例2. 已知四边形ABCD，AB∥CD，且AB=AC=AD=a，

BC=b，且2a>b，求BD的长。

解题思路：根据已知条件AB=AC=AD，若以A为圆心，AB为半径作圆，则BD与直径就构成了一个直角三角形，由AB∥CD，可得ED=BC，再由构股定理即可得解。